Chess Vampires: Unraveling the Mysteries of the Castle Strategy

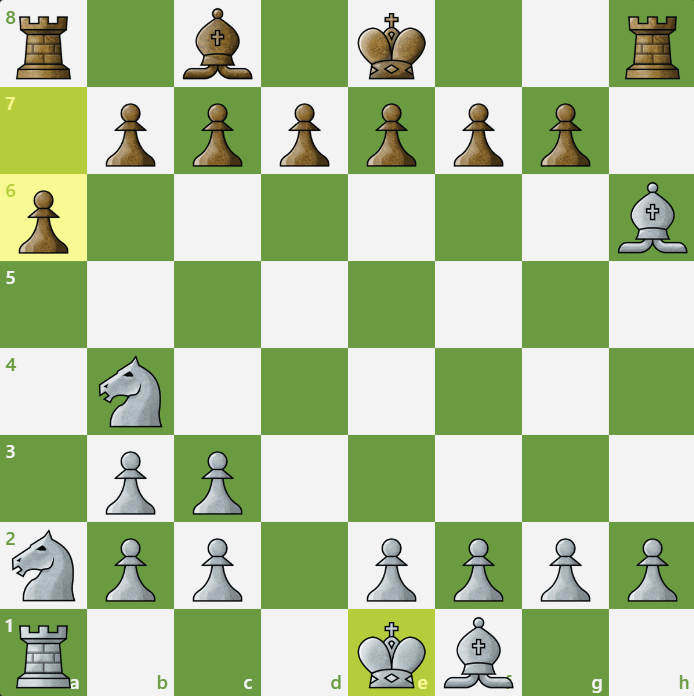
Can you crack this Halloween chess puzzle? 🎃
Hope you had a great Halloween! Here’s a tricky challenge for you: Figure out where the misplaced rook belongs. Is it on g1 or h1?

Only one of the two choices results in a legal chess position (one that could actually occur in a game).

Give it a shot!

Hint: Consider the last moves that might have been played.

So, what’s the connection to Halloween?

Solving this puzzle involves a clever parity argument, which leads us into the eerie world of chess composition: chess vampires.

A chess vampire is a legal position that has no legal mirror image. For more about how a position’s mirror image is defined and to explore these fascinating creatures, visit our first post on chess vampires.

The Vampire’s Castle

Last year, we stumbled upon vampires where en passant was possible. We even explored the woods and uncovered vampires with promoted pieces—rare creatures only found in the darkest hours before dawn. Yet, one mystery lingered.

Could the legend be real? Is there truly a castle of vampires? It’s rumored to lie hidden deep in the shadows, only emerging under the full moon’s glow. Stories of ghostly sightings have kept the legend alive for centuries. Some claim they’ve glimpsed its outline through the trees, while others believe it’s just a myth meant to ward off the curious. Despite many quests, no one had found it.

Today, reader, you have the chance to unveil it. The answer to the puzzle above reveals a castling vampire—a rare creature that survived a castling move. What a remarkable discovery!

Solution:

To solve this, let’s follow the hint and temporarily ignore the rook. We need to figure out the sequence of moves that led to the current puzzle position.

It’s Black’s turn, so White made the last move. While there seem to be several possible retractions for White, we need to determine what Black’s previous move was. If it was a7-a6, what came before that? We need a Black knight to reappear on the board so it can continue retracting.

Both of Black’s knights were captured on b3 and c3.

It would take 3 retractions from White to bring back a Black knight on b3. That’s too many… We also can’t retract dxc3 until the white bishop returns to c1. It seems we’ve hit a wall. But wait! We can gain an extra retraction by bringing a Black pawn back to h6 when retracting the bishop.

From this, we can deduce that the last 5 moves (plies) must have been as follows (still ignoring the rook):

Let’s wrap it up with our standard counting argument. Setting aside the rook for a moment, to arrive at the position just before the move dxc3:

White has made an odd number of moves (an even count of knight moves plus one pawn move, axb3).
Black has made an even number of moves (since squares b3 and c3 are of different colors).
However, in a position where it’s White’s turn to move, both players must have completed an equal number of moves. Thus, we need to adjust White’s move count, which is only possible by placing the rook on g1.

Final Thoughts

This composition answers the age-old question: can there be vampires in a game where castling has occurred? It’s incredible to discover that they do exist.

This revelation also affects how we classify these “vampires” into different “clans,” but that’s a story for another day.

We hope you found this post enjoyable! If you did, don’t forget to share it with your friends. Happy puzzling!